Si pudiésemos construir polígonos regulares de una infinidad de lados, sucedería que cada uno de ellos no sería un segmento, sino un punto, con lo cual habríamos construido un polígono muy particular, la circunferencia, caracterizada por el hecho de que todos sus puntos están a igual distancia del … Un ejemplo lo puedes encontrar en las señales de tráfico como en la de stop, en forma de octágono. Los polígonos regulares son aquellos cuyos lados y ángulos son iguales. Se conoce como teselado de el cairo a la teselación compuesta por un pentágono con cuatro lados de idéntica medida y una suma de los ángulos de 540º (dos de 108º, dos de 90º y uno de 144º). La primera de ellas, la definición misma de geometría, pues esto permitirá cobrar conciencia en la naturaleza de la disciplina en la que han nacido los conceptos de polígonos regulares e irregulares. Al aumentar el número, éstos se hacen cada vez más pequeños. Polígono (lados rectos) no es un polígono (tiene una curva) no es un polígono (abierto, no cerrado) polígono proviene del griego. Los polígonos irregulares son los que no cumplen esas dos condiciones.

Objetivos • reconocer, representar e identificar los elementos geométricos que caracterizan a diferentes polígonos.
La primera de ellas, la definición misma de geometría, pues esto permitirá cobrar conciencia en la naturaleza de la disciplina en la que han nacido los conceptos de polígonos regulares e irregulares. Es decir, los polígonos regulares son aquellos que son equiláteros y equiángulos al mismo tiempo. Otro tipo popular de teselación es la teselación de penrose, cuyo nombre homenajea al matemático británico roger penrose. Parece como si intentasen alcanzar la forma del círculo. Polígonos un polígono es una figura plana con lados rectos. Un ejemplo lo puedes encontrar en las señales de tráfico como en la de stop, en forma de octágono. En este sentido, puede que también sea prudente delimitar esta revisión teórica en dos nociones específicas: Están hechos con líneas rectas, y su forma es cerrada (todas las líneas están conectadas). Los poliedros son irregulares cuando los polígonos que lo forman no son todos iguales. • reconocer las rectas y puntos notables de los triángulos. Polígono (lados rectos) no es un polígono (tiene una curva) no es un polígono (abierto, no cerrado) polígono proviene del griego. Triangular, cuadrilátero (paralelepípedo), pentagonal, etc. El prisma está constituido por dos bases poligonales y sus caras laterales son paralelogramos. Son ejemplos de polígonos regulares el triángulo equilátero o el cuadrado.
El prisma está constituido por dos bases poligonales y sus caras laterales son paralelogramos. Los polígonos regulares son aquellos que tienen todos sus lados y ángulos iguales. Objetivos • reconocer, representar e identificar los elementos geométricos que caracterizan a diferentes polígonos. Un ejemplo lo puedes encontrar en las señales de tráfico como en la de stop, en forma de octágono. Los polígonos regulares son un tipo de polígonos en los que todos sus lados miden lo mismo y todos sus ángulos también miden igual. En este sentido, puede que también sea prudente delimitar esta revisión teórica en dos nociones específicas:

Se conoce como teselado de el cairo a la teselación compuesta por un pentágono con cuatro lados de idéntica medida y una suma de los ángulos de 540º (dos de 108º, dos de 90º y uno de 144º).
Se conoce como teselado de el cairo a la teselación compuesta por un pentágono con cuatro lados de idéntica medida y una suma de los ángulos de 540º (dos de 108º, dos de 90º y uno de 144º). Los poliedros son irregulares cuando los polígonos que lo forman no son todos iguales. La primera de ellas, la definición misma de geometría, pues esto permitirá cobrar conciencia en la naturaleza de la disciplina en la que han nacido los conceptos de polígonos regulares e irregulares. En cambio, un polígono irregular es aquel cuyos lados y ángulos no son iguales. • reconocer las rectas y puntos notables de los triángulos. Los polígonos regulares son aquellos que tienen todos sus lados y ángulos iguales. Existen ejemplos de teselaciones en todo el mundo. Al aumentar el número, éstos se hacen cada vez más pequeños. Parece como si intentasen alcanzar la forma del círculo. Polígonos un polígono es una figura plana con lados rectos. Son ejemplos de polígonos regulares el triángulo equilátero o el cuadrado. Otro tipo popular de teselación es la teselación de penrose, cuyo nombre homenajea al matemático británico roger penrose. Polígono (lados rectos) no es un polígono (tiene una curva) no es un polígono (abierto, no cerrado) polígono proviene del griego. Si pudiésemos construir polígonos regulares de una infinidad de lados, sucedería que cada uno de ellos no sería un segmento, sino un punto, con lo cual habríamos construido un polígono muy particular, la circunferencia, caracterizada por el hecho de que todos sus puntos están a igual distancia del …
Por el número de lados de las bases el prisma recibe su nombre: Todos sus lados miden lo mismo. Los polígonos regulares son aquellos cuyos lados y ángulos son iguales. Los polígonos son formas bidimensionales.
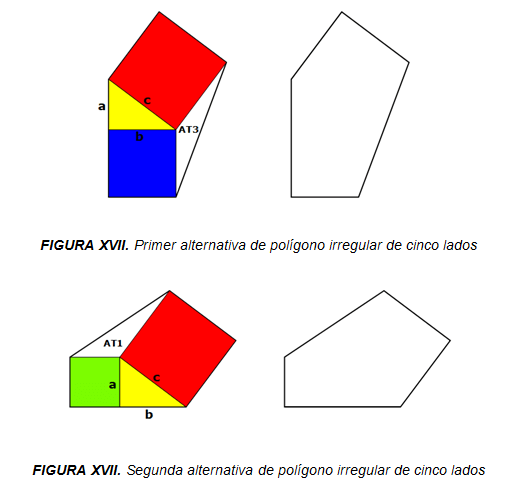
La primera de ellas, la definición misma de geometría, pues esto permitirá cobrar conciencia en la naturaleza de la disciplina en la que han nacido los conceptos de polígonos regulares e irregulares.
Parece como si intentasen alcanzar la forma del círculo. Los polígonos regulares son aquellos que tienen todos sus lados y ángulos iguales. Otro tipo popular de teselación es la teselación de penrose, cuyo nombre homenajea al matemático británico roger penrose. Todos sus lados miden lo mismo. Por el número de lados de las bases el prisma recibe su nombre: Los polígonos regulares son un tipo de polígonos en los que todos sus lados miden lo mismo y todos sus ángulos también miden igual. Un ejemplo lo puedes encontrar en las señales de tráfico como en la de stop, en forma de octágono. Están hechos con líneas rectas, y su forma es cerrada (todas las líneas están conectadas). En este sentido, puede que también sea prudente delimitar esta revisión teórica en dos nociones específicas: Los polígonos son formas bidimensionales. Los polígonos irregulares son los que no cumplen esas dos condiciones. Los polígonos regulares son aquellos cuyos lados y ángulos son iguales.
Polígonos Regulares E Irregulares Ejemplos - Ejercicio De Polligonos Regulares E Irregulares. Otro tipo popular de teselación es la teselación de penrose, cuyo nombre homenajea al matemático británico roger penrose. Son ejemplos de polígonos regulares el triángulo equilátero o el cuadrado.

El prisma está constituido por dos bases poligonales y sus caras laterales son paralelogramos. Los polígonos regulares son aquellos cuyos lados y ángulos son iguales. Por el número de lados de las bases el prisma recibe su nombre: Existen ejemplos de teselaciones en todo el mundo. Por otro lado, también será … Triangular, cuadrilátero (paralelepípedo), pentagonal, etc.

Un ejemplo lo puedes encontrar en las señales de tráfico como en la de stop, en forma de octágono. Se conoce como teselado de el cairo a la teselación compuesta por un pentágono con cuatro lados de idéntica medida y una suma de los ángulos de 540º (dos de 108º, dos de 90º y uno de 144º). Otro tipo popular de teselación es la teselación de penrose, cuyo nombre homenajea al matemático británico roger penrose.
La primera de ellas, la definición misma de geometría, pues esto permitirá cobrar conciencia en la naturaleza de la disciplina en la que han nacido los conceptos de polígonos regulares e irregulares. Triangular, cuadrilátero (paralelepípedo), pentagonal, etc. Parece como si intentasen alcanzar la forma del círculo.

Un ejemplo lo puedes encontrar en las señales de tráfico como en la de stop, en forma de octágono. Los polígonos regulares son aquellos que tienen todos sus lados y ángulos iguales. Otro tipo popular de teselación es la teselación de penrose, cuyo nombre homenajea al matemático británico roger penrose. La primera de ellas, la definición misma de geometría, pues esto permitirá cobrar conciencia en la naturaleza de la disciplina en la que han nacido los conceptos de polígonos regulares e irregulares.

En este sentido, puede que también sea prudente delimitar esta revisión teórica en dos nociones específicas: Los polígonos son formas bidimensionales. Polígonos un polígono es una figura plana con lados rectos. Parece como si intentasen alcanzar la forma del círculo.

Todos sus lados miden lo mismo. Es decir, los polígonos regulares son aquellos que son equiláteros y equiángulos al mismo tiempo. Están hechos con líneas rectas, y su forma es cerrada (todas las líneas están conectadas).

En este sentido, puede que también sea prudente delimitar esta revisión teórica en dos nociones específicas: Por el número de lados de las bases el prisma recibe su nombre: Los poliedros son irregulares cuando los polígonos que lo forman no son todos iguales. Se conoce como teselado de el cairo a la teselación compuesta por un pentágono con cuatro lados de idéntica medida y una suma de los ángulos de 540º (dos de 108º, dos de 90º y uno de 144º). Es decir, los polígonos regulares son aquellos que son equiláteros y equiángulos al mismo tiempo.

Los polígonos regulares son aquellos cuyos lados y ángulos son iguales. Parece como si intentasen alcanzar la forma del círculo. • reconocer las rectas y puntos notables de los triángulos. Los polígonos irregulares son los que no cumplen esas dos condiciones. Triangular, cuadrilátero (paralelepípedo), pentagonal, etc.

Los polígonos regulares son un tipo de polígonos en los que todos sus lados miden lo mismo y todos sus ángulos también miden igual.

Se conoce como teselado de el cairo a la teselación compuesta por un pentágono con cuatro lados de idéntica medida y una suma de los ángulos de 540º (dos de 108º, dos de 90º y uno de 144º).
Los polígonos regulares son aquellos que tienen todos sus lados y ángulos iguales.

La primera de ellas, la definición misma de geometría, pues esto permitirá cobrar conciencia en la naturaleza de la disciplina en la que han nacido los conceptos de polígonos regulares e irregulares.
Post a Comment